平面向量习题|高阶

前言

在高中阶段，平面向量是个非常特殊的数学素材，在没有引入向量的坐标时，我们一般会想到用“形”来刻画向量，它们之间的加减运算主要依托“三角形法则”和“平行四边形法则”展开；当引入了向量的坐标表示以后，向量就有了“数”的内涵，这时候向量之间的运算，即可以考虑用“形”来刻画，也可以考虑用数来刻画。
比如用形来刻画运算，$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}=\vec{0}$，$\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BC}$等，
再比如用数来刻画运算，设$\vec{a}=(x_1，y_1)$，$\vec{b}=(x_2，y_2)$；则$\vec{a}\pm \vec{b}=(x_1\pm x_2，y_1\pm y_2)$，$\vec{a}\cdot \vec{b}=x_1x_2+y_1y_2$；
再比如用数来刻画位置关系，$\vec{a}//\vec{b}\Leftrightarrow x_1y_2-x_2y_1=0$；$\vec{a}\perp \vec{b}\Leftrightarrow x_1x_2+y_1y_2=0$；

典例剖析

设$O$在$\Delta ABC$内部，且有$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}$，则$\Delta ABC$的面积与$\Delta AOC$的面积之比为多少？

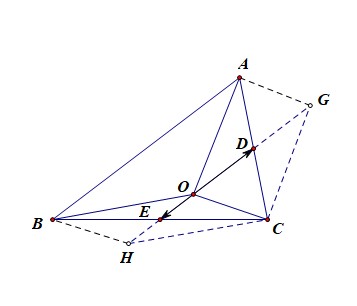
分析：由题目可知$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}$，

将其系数做恰当的拆分得到，$(\overrightarrow{OA}+\overrightarrow{OC})+2(\overrightarrow{OB}+\overrightarrow{OC})=\vec{0}$，

如图即$2\overrightarrow{OD}=-4\overrightarrow{OE}$，即$\overrightarrow{OD}=-2\overrightarrow{OE}$，

即可知点$O$一定在$\Delta ABC$的中位线$DE$上，且在中位线上靠近点$E$的三等分点处。

理由如下：以$OA$和$OC$为邻边做平行四边形$AOCG$，则点$D$为$AC$的中点，

同理，点$E$为$BC$的中点，则可知$DE$为中位线，又$\overrightarrow{OD}=-2\overrightarrow{OE}$，

则$O、D、E$三点共线，故点$O$一定在$\Delta ABC$的中位线$DE$上，且在中位线上靠近点$E$的三等分点处。

令点$B$到边$AC$的高线为$h$，则过点$E$和边$AC$平行的直线必然会平分高线$h$，

又由于点$O$是$DE$的三等分点之一，故$\triangle AOC$ 的高为$\cfrac{h}{2}$的$\cfrac{2}{3}$，

则$S_{\Delta ABC}=\cfrac{1}{2}\cdot AC\cdot h$，$S_{\Delta AOC}=\cfrac{1}{2}\cdot AC\cdot \cfrac{h}{2}\cdot \cfrac{2}{3}=\cfrac{1}{3}\cdot\cfrac{1}{2}\cdot AC\cdot h$，

故$\Delta ABC$的面积与$\Delta AOC$的面积之比为3。

【反思总结】：线段等分点的向量给出方式，

二等分点(中点)：$\overrightarrow{OA}=-\overrightarrow{OB}$，或$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}$，则点$O$是$AB$的中点；

三等分点：$\overrightarrow{OA}=-2\overrightarrow{OB}$，或$\overrightarrow{OA}+2\overrightarrow{OB}=\overrightarrow{0}$，则点$O$是$AB$的靠近$B$的三等分点；

四等分点：$\overrightarrow{OA}=-3\overrightarrow{OB}$，或$\overrightarrow{OA}+3\overrightarrow{OB}=\overrightarrow{0}$，则点$O$是$AB$的靠近$B$的四等分点；

设$O$在$\Delta ABC$内部，且有$\overrightarrow{OA}=2\overrightarrow{BO}+3\overrightarrow{CO}$，延长$BO$交$AC$于点$D$，则$\cfrac{S_{\Delta COD}}{S_{\Delta AOD}}$的值为【B】

$A.\cfrac{2}{3}$ $B.\cfrac{1}{3}$ $C.\cfrac{1}{2}$ $D.\cfrac{3}{4}$

分析：由题目可知$\overrightarrow{OA}+2\overrightarrow{OB}+3\overrightarrow{OC}=\vec{0}$，

将其系数做恰当的拆分得到，$(\overrightarrow{OA}+\overrightarrow{OC})+2(\overrightarrow{OB}+\overrightarrow{OC})=\vec{0}$，

如图即$2\overrightarrow{OF}=-4\overrightarrow{OE}$，即$\overrightarrow{OF}=-2\overrightarrow{OE}$，

即可知$E、O、F$三点共线，且点$O$一定在$\Delta ABC$的中位线$EF$上，且在中位线上靠近点$E$的三等分点处。

理由如下：以$OA$和$OC$为邻边做平行四边形$AOCG$，则点$F$为$AC$的中点，

同理，点$E$为$BC$的中点，则可知$EF$为中位线，又$\overrightarrow{OF}=-2\overrightarrow{OE}$，

则$E、O、F$三点共线，故点$O$一定在$\Delta ABC$的中位线$EF$上，且在中位线上靠近点$E$的三等分点处。

此时连结$BE$，由点$O$是$\triangle BCF$的重心可知，延长$BO$交$AC$于点$D$，

则点$D$必是边$CF$的中点，即$CD=DF$，则$AD=2DF=3CD$，

过点$O$作$AC$的垂线段，设其高为$h$，

由同高不同底可得，$\cfrac{S_{\Delta COD}}{S_{\Delta AOD}}=\cfrac{\cfrac{1}{2}\cdot CD\cdot h}{\cfrac{1}{2}\cdot AD\cdot h}=\cfrac{1}{3}$

【解后反思】当题目告诉$\overrightarrow{OA}=2\overrightarrow{BO}+3\overrightarrow{CO}$，则有结论：

①$E、O、F$三点共线，点$O$一定在$\Delta ABC$的中位线$EF$上，且在中位线上靠近点$E$的三等分点处。

②延长$BO$交$AC$与点$D$，则点$D$是$CF$的中点。

③三等分点出现，常常和三角形的重心，三角形边的中点等联系起来，

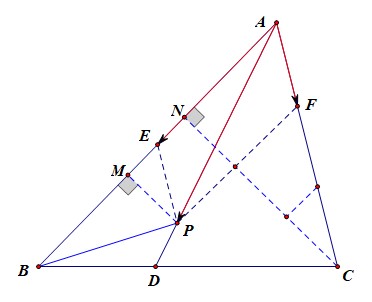
设$P$在$\Delta ABC$内部，且有$\overrightarrow{AP}=\cfrac{1}{2}\cdot \overrightarrow{AB}+\cfrac{1}{3}\cdot\overrightarrow{AC}$，则$\cfrac{S_{\Delta ABP}}{S_{\Delta ABC}}$的值为【B】

$A.\cfrac{2}{3}$ $B.\cfrac{1}{3}$ $C.\cfrac{1}{2}$ $D.\cfrac{3}{4}$

分析：如图，点$E$，$F$分别是边$AB$，$AC$的二等分点和三等分点，作平行四边形$AEPF$，延长$AP$交$BC$于点$D$，

则由图可知，$\triangle ABP$的高$PM$与$\triangle ABC$的高$CN$的关系为$CN=3PM$，

故由同底不同高可知，$\cfrac{S_{\Delta ABP}}{S_{\Delta ABC}}=\cfrac{\cfrac{1}{2}\cdot PM\cdot AB}{\cfrac{1}{2}\cdot CN\cdot AB}=\cfrac{1}{3}$

引申：且可知$3BD=2CD$。

【三角形重心的给出方式】在$\Delta ABC$中，$\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD}$，则点$D$为$\triangle ABC$的重心。

分析：如图所示，

由于$\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD}$，

又$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}=2\overrightarrow{AF}=2\cdot \cfrac{3}{2}\overrightarrow{AD}=3\overrightarrow{AD}$，

故点$D$为$\triangle ABC$的重心，

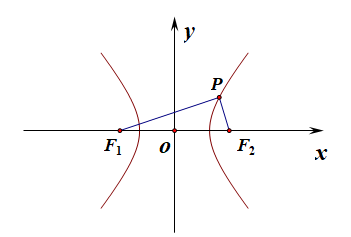
设F$_1$、F$_2$为双曲线$\cfrac{x^2}{a^2}-\cfrac{y^2}{b^2}=1(a>0，b>0)$的左右焦点，$P$为双曲线右支上的一点，满足$(\overrightarrow{OP}+\overrightarrow{OF_2})\cdot \overrightarrow{PF_2}=0$，$O$为坐标原点，且$3|\overrightarrow{PF_1}|=4|\overrightarrow{PF_2}|$，则双曲线的离心率是多少？

分析：设点$P(x，y)$，由点$F_1(-c，0)$和点$F_2(c，0)$，得到$\overrightarrow{OP}=(x，y)$，$\overrightarrow{OF_2}=(c，0)$，

$\overrightarrow{OP}+\overrightarrow{OF_2}=(c+x，y)$，$\overrightarrow{PF_1}=(-c-x，-y)$，$\overrightarrow{PF_2}=(c-x，-y)$，

由$(\overrightarrow{OP}+\overrightarrow{OF_2})\cdot \overrightarrow{PF_2}=0$得到，

$(c-x)(c+x)-y^2=0$，即$c^2=x^2+y^2$，

即点$P$在以坐标原点为圆心，以$c$为半径的圆上；

也在以$F_1F_2$为直径的圆上，故$\angle F_1PF_2=90^{\circ}$。

【初中数学：直径所对的圆周角为直角】

故有$\overrightarrow{PF_1}\cdot \overrightarrow{PF_2}=0$，

这样$3|\overrightarrow{PF_1}|=4|\overrightarrow{PF_2}|$得到，

可设$|PF_1|=4k(k>0)$，$|PF_2|=3k$，故$|F_1F_2|=5k$，即$2c=5k$，

又由双曲线的定义知道，$|PF_1|-|PF_2|=2a=k$ ，

则离心率$e=\cfrac{2c}{2a}=\cfrac{5k}{k}=5$。

【点评】①用向量的左边引入数学运算，从而能得到点$P$的轨迹，这样就能得出直角三角形。

②由直角三角形结合已知条件能得到$2c$，用定义式能得到$2a$，从而离心率可解。

【2017辽宁沈阳二模】已知向量$\overrightarrow{OA}=(3，1)$，$\overrightarrow{OB}=(-1，3)$，$\overrightarrow{OC}=m\overrightarrow{OA}$$-n\overrightarrow{OB}$$(m>0，n>0)$，若$m+n\in [1，2]$，则向量$|\overrightarrow{OC}|$的取值范围是【】

$A.[\sqrt{5}，2\sqrt{5}]$ $B.[\sqrt{5}，2\sqrt{10})$ $C.(\sqrt{5}，\sqrt{10})$ $D.[\sqrt{5}，2\sqrt{10}]$

解：$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}=m(3，1)-n(-1，3)=(3m，m)-(-n，3n)=(3m+n，m-3n)$，

故$|\overrightarrow{OC}|=\sqrt{(3m+n)^2+(m-3n)^2}=\sqrt{10m^2+10n^2}=\sqrt{10}\sqrt{m^2+n^2}$

【预备知识】已知$m>0$，$n>0$ ，$m+n\in [1，2]$，求$m^2+n^2$的取值范围。

分析：将上述给定的数的条件转化为形的条件，则$m^2+n^2$可以看成半径为$r$的动圆上位于第一象限内的一点，$1\leq m+n\leq 2$可以看成两条平行线$m+n=1$和$m+n=2$之间的平面区域内且位于第一象限的的任意一点，

故$m^2+n^2$的取值范围：最小值可以看成圆心$(0，0)$到直线$m+n=1$的距离的平方，最大值可以看成圆心$(0，0)$到点$(0，2)$或$(2，0)$的距离的平方(取不到)，

则可知$d_1=\cfrac{1}{\sqrt{2}}$，$d_2=2$，故$d_1^2=\cfrac{1}{2}$，$d_2^2=4$，即$m^2+n^2\in [\cfrac{1}{2}，4]$；

接上可知，$|\overrightarrow{OC}|=\sqrt{10}\sqrt{m^2+n^2}\in [\sqrt{5}，2\sqrt{10})$，故选$B$。

已知向量$\vec{a}=(1，1)$，$\vec{b}=(-1，1)$，$\vec{c}=(\sqrt{2}cos\theta，\sqrt{2}sin\theta)$，实数$m，n$满足$m\vec{a}+n\vec{b}=\vec{c}$，则$(m-1)^2+(n-1)^2$的最小值为$3-2\sqrt{2}$；

法1：由于$m\vec{a}+n\vec{b}=\vec{c}$，即$m(1，1)+n(-1，1)=(\sqrt{2}cos\theta，\sqrt{2}sin\theta)$

则$\left\{\begin{array}{l}{m-n=\sqrt{2}cos\theta}\\{m+n=\sqrt{2}sin\theta}\end{array}\right.$，借助$cos^2\theta+sin^2\theta=1$可得，

$(m+n)^2+(m-n)^2=2$，打开整理得到$m^2+n^2=1$，

故$(m-1)^2+(n-1)^2=m^2+n^2-2(m+n)+2=3-2\sqrt{2}sin\theta$，

由于$-1\leq sin\theta\leq 1$，则$3-2\sqrt{2}\leq 3-2\sqrt{2}sin\theta\leq 3+2\sqrt{2}$

故所求的最小值为$3-2\sqrt{2}$。

法2：变量集中，由$\left\{\begin{array}{l}{m-n=\sqrt{2}cos\theta}\\{m+n=\sqrt{2}sin\theta}\end{array}\right.$，

解得$m=\cfrac{\sqrt{2}(cos\theta+sin\theta)}{2}$，$n=\cfrac{\sqrt{2}(sin\theta-cos\theta)}{2}$，

代入得到$(m-1)^2+(n-1)^2=\Big[\cfrac{\sqrt{2}(cos\theta+sin\theta)}{2}-1\Big]^2+\Big[\cfrac{\sqrt{2}(sin\theta-cos\theta)}{2}-1\Big]^2$

$=3-2\sqrt{2}sin\theta$；其余同上；

【均值不等式的使用】在平面直角坐标系$xoy$中，已知点$A$在椭圆$\cfrac{x^2}{16}+\cfrac{y^2}{8}=1$上，点$P$满足$\overrightarrow{AP}=(\lambda-1)\overrightarrow{OA}(\lambda\in R)$，且$\overrightarrow{OA}\cdot \overrightarrow{OP}=12$，求线段$OP$在$x$轴上的投影长度的最大值。

解析：由$\overrightarrow{AP}=(\lambda-1)\overrightarrow{OA}$，即$\overrightarrow{OP}-\overrightarrow{OA}=(\lambda-1)\overrightarrow{OA}$

则有$\overrightarrow{OP}=\lambda\overrightarrow{OA}$，故$O、P、A$三点共线，由$\overrightarrow{OA}\cdot \overrightarrow{OP}=12$，得到$|\overrightarrow{OA}|\cdot |\overrightarrow{OP}|=12$，

设OP与$x$轴的夹角为$\theta$，点$A(x，y)$，$B$为点$A$在$x$轴上的投影，由图可知，线段$OP$在$x$轴上的投影长度为$||\overrightarrow{OP}|\cdot cos\theta|$

则$||\overrightarrow{OP}|\cdot cos\theta|=|\overrightarrow{OP}|\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}$$=\cfrac{12}{|\overrightarrow{OA}|}\times \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}$

$=12\cdot \cfrac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|^2}$，又由于$|\overrightarrow{OB}|=|x|$，$|\overrightarrow{OA}|=\sqrt{x^2+y^2}$，

$=12\times \cfrac{|x|}{x^2+y^2}$，接下来施行变量集中，由于$\cfrac{x^2}{16}+\cfrac{y^2}{8}=1$，得到$y^2=8-\cfrac{x^2}{2}$，代入

$=12\times \cfrac{|x|}{\cfrac{x^2}{2}+8}$，分子分母同除以$|x|$得到，

$=12\times \cfrac{1}{\frac{|x|}{2}+\frac{8}{|x|}}\leq 12\times \cfrac{1}{4}=3$，

当且仅当$|x|=4$时等号成立，故线段$OP$在$x$轴上的投影长度的最大值为$3$。

【向量的模的运算】已知$|\vec{a}|=1，|\vec{b}|=2，<\vec{a}，\vec{b}>=60^{\circ}$，求$|\vec{a}+2\vec{b}|$

法1：基向量法，

$|\vec{a}+2\vec{b}|^2=\vec{a}^2+4\vec{b}^2+2\times 2\times \vec{a}\cdot \vec{b}$；

$=|\vec{a}|^2+4|\vec{b}|^2+4|\vec{a}|\cdot |\vec{b}|\cdot cos60^{\circ}$；

$=1+16+4\times 1\times 2\times cos60^{\circ}=21$，

故$|\vec{a}+2\vec{b}|=\sqrt{21}$。

法2：建立坐标系，利用向量坐标法构造向量三角形法，

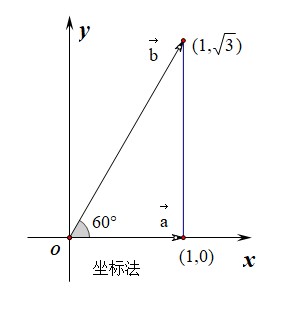
建立如图所示的坐标系，则可知$\vec{a}=(1，0)$，$\vec{b}=(1，\sqrt{3})$，

则$\vec{a}+2\vec{b}=(1，0)+2(1，\sqrt{3})=(3，2\sqrt{3})$，

故$|\vec{a}+2\vec{b}|=\sqrt{3^2+(2\sqrt{3})^2}=\sqrt{21}$。

法3：构造向量三角形法，利用余弦定理求解。

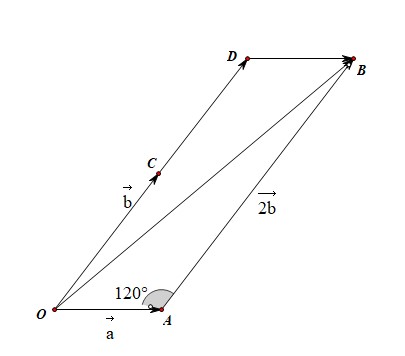
由图可知，$\overrightarrow{OA}=\vec{a}$，$\overrightarrow{OD}=2\vec{b}$，做向量三角形$\triangle OAB$，

则在$\triangle OAB$中，$|OA|=|\vec{a}|=1$，$|AB|=|2\vec{b}|=4$，$|OB|=|\vec{a}+2\vec{b}|$，$\angle OAB=120^{\circ}$，

由余弦定理可知，$|OB|^2=1^2+4^2-2\times 1\times 4\times cos120^{\circ}=21$，

故$|\vec{a}+2\vec{b}|=|OB|=\sqrt{21}$。

【向量共面基本定理+同一法】在$\triangle ABC$中，点$G$满足$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$，若存在点$O$，使得$\overrightarrow{OG}=\cfrac{1}{6}\overrightarrow{BC}$，且$\overrightarrow{OA}=m\overrightarrow{OB}+n\overrightarrow{OC}$，则$m-n$=【】

$A.2$ $B.-2$ $C.1$ $D.-1$

分析：由题目$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$可知，

$(\overrightarrow{OA}-\overrightarrow{OG})+(\overrightarrow{OB}-\overrightarrow{OG})+(\overrightarrow{OC}-\overrightarrow{OG})=\vec{0}$，整理得到

$\overrightarrow{OG}=\cfrac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})$，又$\overrightarrow{OG}=\cfrac{1}{6}\overrightarrow{BC}$，

则$\cfrac{1}{3}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC})=\cfrac{1}{6}\overrightarrow{BC}=\cfrac{1}{6}(\overrightarrow{OC}-\overrightarrow{OB})$

整理得到，$\overrightarrow{OA}=-\cfrac{3}{2}\overrightarrow{OB}-\cfrac{1}{2}\overrightarrow{OC}$，结合已知$\overrightarrow{OA}=m\overrightarrow{OB}+n\overrightarrow{OC}$，

则可知$m=-\cfrac{3}{2}$，$n=-\cfrac{1}{2}$，则$m-n=-1$，故选$D$。

【2017年理科数学全国卷Ⅲ卷第12题】在矩形$ABCD$中，$AB=1$，$AD=2$，动点$P$在以$C$为圆心且与$BD$相切的圆上，若$\overrightarrow{AP}=\lambda \overrightarrow{AB}+\mu \overrightarrow{AD}$，则$\lambda+\mu$的最大值为【】

$A.3$ $B.2\sqrt{2}$ $C.\sqrt{5}$ $D.2$

分析：以点$A$为坐标原点，分别以$AD$，$AB$所在的直线为$x$轴和$y$轴建立如图所示的平面直角坐标系，则$A(0，0)$，$B(0，1)$，$C(2，1)$，$D(2，0)$；

又由于$AB=1$，$AD=2$，动点$P$在以$C$为圆心且与$BD$相切的圆上，则$BD=\sqrt{5}$，由等面积法可知圆的半径为$r=\cfrac{2}{\sqrt{5}}$，

这样圆上的动点的坐标可设为$P(2+\cfrac{2}{\sqrt{5}}cos\theta，1+\cfrac{1}{\sqrt{5}}cos\theta)$，

由于$\overrightarrow{AP}=\lambda \overrightarrow{AB}+\mu \overrightarrow{AD}=\lambda(0，1)+\mu(2，0)=(2\mu，\lambda)$，

又由于$\overrightarrow{AP}=(2+\cfrac{2}{\sqrt{5}}cos\theta，1+\cfrac{2}{\sqrt{5}}sin\theta)$，则有

$2\mu=2+\cfrac{2}{\sqrt{5}}cos\theta$，$\lambda=1+\cfrac{2}{\sqrt{5}}sin\theta$，

化简为$\mu=1+\cfrac{1}{\sqrt{5}}cos\theta$，$\lambda=1+\cfrac{2}{\sqrt{5}}sin\theta$，

则$\lambda+\mu=1+\cfrac{1}{\sqrt{5}}cos\theta+1+\cfrac{2}{\sqrt{5}}sin\theta=2+\cfrac{1}{\sqrt{5}}cos\theta+\cfrac{2}{\sqrt{5}}sin\theta=2+sin(\theta+\phi)$，

由于$-1\leq sin(\theta+\phi)\leq 1$，故$2-1\leq 2+sin(\theta+\phi)\leq 2+1$，即$\lambda+\mu\in [1，3]$，

故所求的最大值为3，故选$A$。

解后反思：培养主动使用向量这一数学工具的数学应用意识很关键。

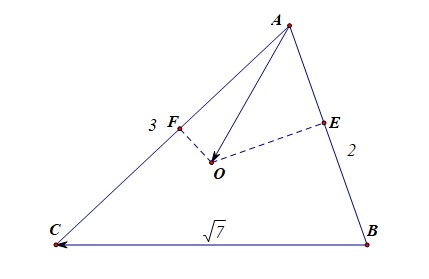
已知点$O$是$\triangle ABC$的外接圆的圆心，$AC=3$，$AB=2$，$BC=\sqrt{7}$，求$\overrightarrow{AO}\cdot \overrightarrow{BC}$的值；

分析：本题目可以考虑的角度比较多，比如利用向量的内积的定义，向量的内积的坐标运算，这些思路都不能走下去，所以需要重新思考新的思路，比如利用向量的内积的几何意义；

由于点$O$是外心，过点$O$做$OF\perp AC$于点$F$，过点$O$做$OE\perp AB$于点$E$，则$|AF|=\cfrac{3}{2}$，$|AE|=1$，

$\overrightarrow{AO}\cdot \overrightarrow{BC}=\overrightarrow{AO}\cdot (\overrightarrow{AC}-\overrightarrow{AB})=\overrightarrow{AO}\cdot \overrightarrow{AC}-\overrightarrow{AO}\cdot \overrightarrow{AB}$

$=|\overrightarrow{AO}||\overrightarrow{AC}|cos\angle CAO-|\overrightarrow{AO}||\overrightarrow{AB}|cos\angle BAO=|\overrightarrow{AC}||\overrightarrow{AF}|-|\overrightarrow{AB}||\overrightarrow{AE}|$

$=3\times \cfrac{3}{2}-2\times 1=\cfrac{5}{2}$。

【2019届高三理科数学三轮模拟试题】已知$\triangle ABC$的内角$A$，$B$，$C$所对的边分别是$a$、$b$、$c$，且满足$(b+2c)cosA=-acosB$，设$D$为$BC$的中点，$b=4$，$AD=\sqrt{7}$，则$c$= 【】

【法1】：如图所示，由$(b+2c)cosA=-acosB$，边化角，得到$A=120^{\circ}$，设$BD=CD=y$，$AB=x$，$\angle ADB=\alpha$，$\angle ADC=\beta$，

在$\triangle ABC$中，$AB=x$，$AC=4$，$BC=2y$，$A=120^{\circ}$，

则由余弦定理得到$(2y)^2=x^2+16-2\cdot 4x\cdot cos120^{\circ}$①，

又在$\triangle ADB$和$\triangle ADC$中，由$cos\alpha+cos\beta=0$，得到$\cfrac{7+y^2-x^2}{2\sqrt{7}y}+\cfrac{7+y^2-16}{2\sqrt{7}y}=0$②，

联立①②，得到$x=6$或$x=-2$(舍去)，故选$A$。

【法2】：由$(b+2c)cosA=-acosB$，边化角，得到$A=120^{\circ}$，由于点$D$为$BC$的中点，利用向量方法，

$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}$，两边平方，得到

$|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2+2|\overrightarrow{AB}|\cdot |\overrightarrow{AC}|cos120^{\circ}=4|\overrightarrow{AD}|^2$，即$x^2+16+2\cdot x\cdot 4\cdot (-\cfrac{1}{2})=28$，

化简为$x^2-4x-12=0$，解得$x=6$或$x=-2$(舍去)，故选$A$。

解后反思：法1为通法，法2特殊解法，比如点$D$变化为四分之三等分点，法2就失效了；同时注意，出现$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}$或者$\overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$，意味着点$D$为$BC$的中点。

【2019届高三理科数学三轮模拟试题】已知平面向量$\vec{a}$、$\vec{b}$满足$(\vec{a}-2\vec{b})\perp (3\vec{a}+\vec{b})$，且$|\vec{a}|=\cfrac{1}{2}|\vec{b}|$，则向量$\vec{a}$与$\vec{b}$的夹角的正弦值为【】

$A.\cfrac{1}{2}$ $B.-\cfrac{1}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.-\cfrac{\sqrt{3}}{2}$

分析：由题可知，$(\vec{a}-2\vec{b})\cdot (3\vec{a}+\vec{b})=0$，化简得到，$3\vec{a}^2-5\vec{a}\cdot \vec{b}-2\vec{b}^2=0$①，

由$|\vec{a}|=\cfrac{1}{2}|\vec{b}|$，可设$|\vec{a}|=t(t>0)$，则$|\vec{b}|=2t$，代入①式，

得到$-10t^2cos\theta+5t^2=0$，得到$cos\theta=\cfrac{1}{2}$，则$sin\theta=\cfrac{\sqrt{3}}{2}$，故选$C$.

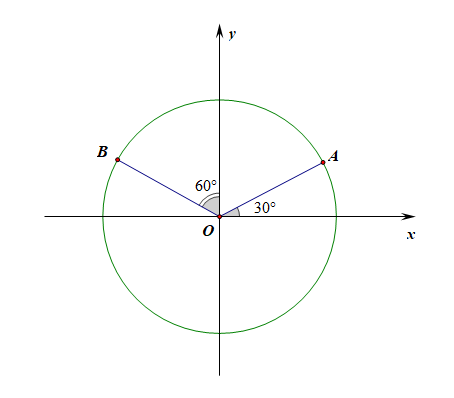
【2019届高三理科数学三轮模拟试题】如图，已知两点$A$，$B$在单位圆上，$\angle yOB=60^{\circ}$，$\angle xOA=30^{\circ}$，则$|2\overrightarrow{OA}+3\overrightarrow{OB}|$=___________。

法1：向量法，由题目可知，$\angle AOB=120^{\circ}$，$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$，

则$|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{|2\overrightarrow{OA}+3\overrightarrow{OB}|^2}$

$=\sqrt{4|\overrightarrow{OA}|^2+9|\overrightarrow{OB}|^2+2\times 2\times 3\times \overrightarrow{OA}\cdot \overrightarrow{OB}}$

$=\sqrt{4+9+2\times 2\times 3\times 1\times 1\times (-\cfrac{1}{2})}=7$，故$|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7}$。

法2：坐标法，已知$A(\cfrac{\sqrt{3}}{2}，\cfrac{1}{2})$，$B(-\cfrac{\sqrt{3}}{2}，\cfrac{1}{2})$，则$\overrightarrow{OA}=(\cfrac{\sqrt{3}}{2}，\cfrac{1}{2})$，

$\overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2}，\cfrac{1}{2})$，则$2\overrightarrow{OA}+3\overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2}，\cfrac{5}{2})$，

故$|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{(-\cfrac{\sqrt{3}}{2})^2+(\cfrac{5}{2})^2}=\sqrt{7}$。

法3：解三角形法，由向量的平行四边形法则可知，所求的模长即$\triangle OCD$中的边长$|OC|$，由已知$|OD|=3|OB|=3$，$|CD|=2|OA|=2$，$\angle ODC=60^{\circ}$，

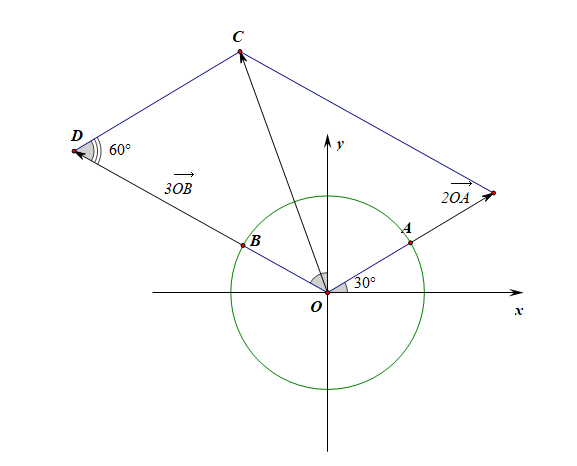
由余弦定理可知$|2\overrightarrow{OA}+3\overrightarrow{OB}|^2=|OC|^2=2^2+3^2-2\times2\times 3\times cos60^{\circ}=7$，

故$|2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7}$。

【2019届高三理科数学三轮模拟试题】已知在平面四边形$MNPQ$中，$\overrightarrow{MP}=(2，4)$，$\overrightarrow{NQ}=(-4，4)$，则$\overrightarrow{MN}\cdot \overrightarrow{PQ}$的最小值为_________.

分析：特殊化策略，由于平面向量是自由向量，故我们可以将点$M$平移到坐标原点，将点$N$放置到$x$轴上，

故点$M(0，0)$，$N(x，0)$，则点$P(2，4)$，可以计算得到点$Q(x-4，0)$，

则$\overrightarrow{MN}=(x，0)$，$\overrightarrow{PQ}=(x-6，-4)$，

故$\overrightarrow{MN}\cdot \overrightarrow{PQ}=(x，0)\cdot(x-6，-4)=x(x-6)=(x-3)^2-9$，

故当$x=3$时，其有最小值为$-9$。

【向量的投影的几何意义】【2018西安八校联考第5题】已知$O$是坐标原点，点$A(2，1)$，点$M(x，y)$是平面区域$\begin{cases}&y\leq x\\&x+y\leq 1\\&y\ge -1\end{cases}$内的一个动点，则$\overrightarrow{OA}\cdot \overrightarrow{OM}$的最大值是多少？

法1：利用向量的坐标运算得到，$\overrightarrow{OA}\cdot \overrightarrow{OM}=2x+y$，故转化为求$2x+y$的最大值，即求$z=2x+y$的最大值，用线性规划的常规方法解决即可。

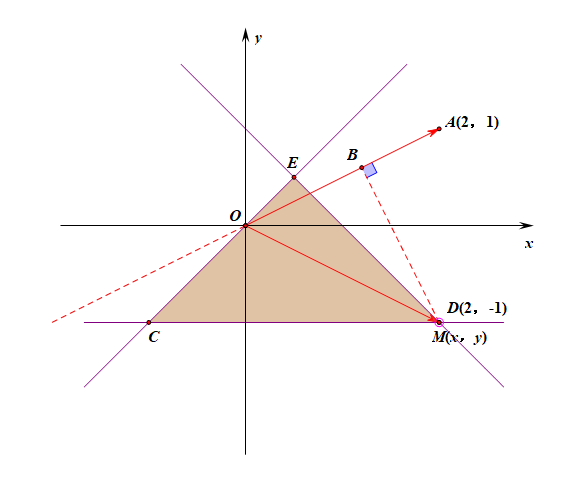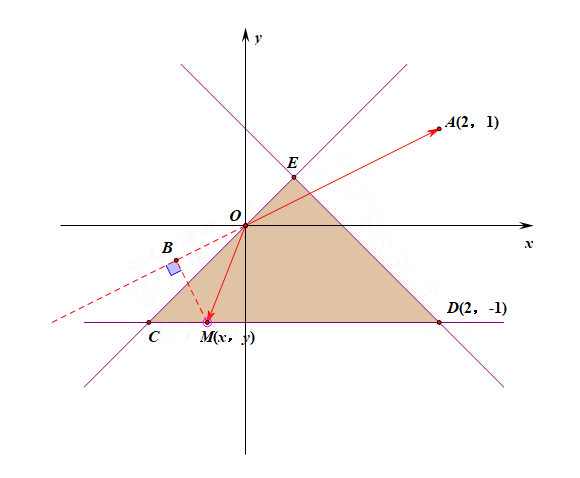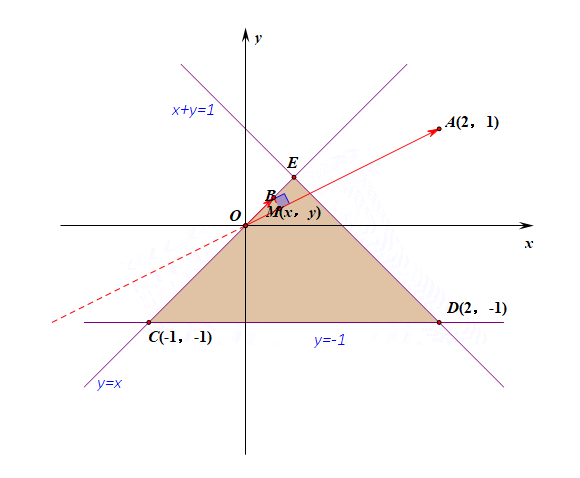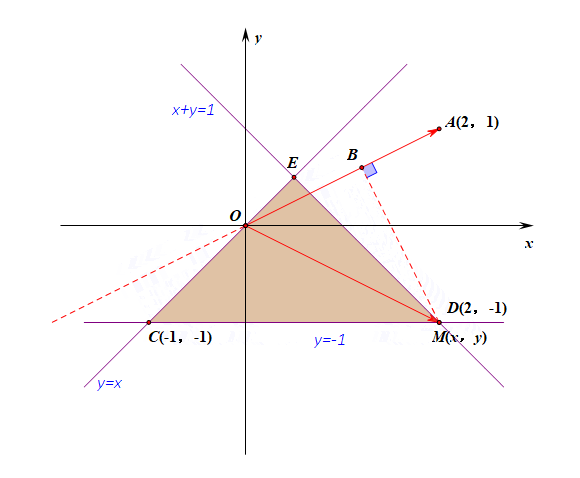
法2：利用向量的投影的几何意义求解，说明：点$M$是三角形区域内部及边界上的一个动点，动画只做了点$M$在边界上的情形；

注：图中有向线段$OB$是向量$\overrightarrow{OM}$在向量$\overrightarrow{OA}$方向上的投影，它是可正，可负，可零的；

$\overrightarrow{OA}\cdot \overrightarrow{OM}=|\overrightarrow{OA}|\cdot |\overrightarrow{OM}|\cdot cos\theta$，其中$|\overrightarrow{OA}|$是个定值，

故只需要求$|\overrightarrow{OM}|\cdot cos\theta$的最大值，而$|\overrightarrow{OM}|\cdot cos\theta$的几何意义是$\overrightarrow{OM}$在$\overrightarrow{OA}$方向上的投影，

由图形可知，当点$M(x，y)$位于点$(2，-1)$时投影$|\overrightarrow{OM}|\cdot cos\theta$最大，故将点$(2，-1)$代入$\overrightarrow{OA}\cdot \overrightarrow{OM}=3$。

变式题：求$\overrightarrow{OA}\cdot \overrightarrow{OM}$的最小值是多少？

分析：由上图可以看出，当两个向量的夹角为钝角时，其投影是负值，故当点$M$位于点$C$时，其内积最小，

此时将点$(-1，-1)$代入得到$\overrightarrow{OA}\cdot \overrightarrow{OM}=-3$。

【2019届高三理科数学三轮模拟试题】已知$A$，$B$是函数$f(x)=\left\{\begin{array}{l}{e^{x-2a}，x\geqslant a}\\{e^{-x}，x<a}\end{array}\right.(a>0)$图像上的两个动点，点$P(a，0)$，若$\overrightarrow{PA}\cdot \overrightarrow{PB}$的最小值为0，则函数$f(x)$的最小值为【】

$A.-\cfrac{1}{e^2}$ $B.-\cfrac{1}{e}$ $C.\cfrac{1}{e^2}$ $D.\cfrac{1}{e}$

分析：先做出分段函数$f(x)$的大致草图如下，

由于分段函数的图像关于$x=a$对称，点$P(a，0)$在对称轴上，故由$\overrightarrow{PA}\cdot \overrightarrow{PB}$的最小值为$0$，

结合图像可知两个向量的夹角为锐角或直角，不可能为钝角，否则最小值为负值，

又由于图像是对称的，从点$P$出发的两条射线都和曲线相切时向量的夹角才会最大，

故说明向量的夹角为$90^{\circ}$，且可知两条切线的斜率为$k=\pm 1$，且可知$\angle APO=45^{\circ}$，

那么怎么说明两个切点就是图中的$A$，$B$两个点呢？

设切点$A(x_0，y_0)$，则$-e^{-x_0}=-1$，则$x_0=0$，$y_0=1$，故点$A(0，1)$，从而可知$a=1$，

由对称性也可知，$B(2，1)$，到此完全说明$A(0，1)$，$B(2，1)$为两个切点。

故$f(x)_{min}=f(a)=f(1)=\cfrac{1}{e}$，故选$D$。

【2019届高三理科数学三轮模拟试题】过圆$O：x^2+y^2=4$外的一点$P$做圆$O$的两条切线，切点分别为$A$，$B$，若$|AB|=2\sqrt{3}$，则$\overrightarrow{PA}\cdot \overrightarrow{PB}$=【】

$A.4$ $B.6$ $C.4\sqrt{3}$ $D.6\sqrt{3}$

分析：如图所示，$|OB|=2$，$|BD|=\cfrac{1}{2}|AB|=\sqrt{3}$，故$\angle BOD=60^{\circ}$，

则$\angle PBO=30^{\circ}$，则两向量$\overrightarrow{PA}$与$\overrightarrow{PB}$的夹角为$\angle APB=60^{\circ}$，

又由于$Rt\triangle BOP$，则$|\overrightarrow{PB}|=2\sqrt{3}$，则有$\overrightarrow{PA}\cdot \overrightarrow{PB}=2\sqrt{3}\times2\sqrt{3}\times cos60^{\circ}=6$，故选$B$.

【2019届高三理科数学三轮模拟试题】在平面直角坐标系$xOy$中，已知点$A(1，0)$，点$B(0，1)$，$\angle AOC=30^{\circ}$，设$\overrightarrow{OC}=m\overrightarrow{OA}+n\overrightarrow{OB}$，且点$C$在第一象限，则$\cfrac{m}{n}$=_________。

分析：$\cfrac{m}{n}=\sqrt{3}$。

【2014.浙江卷】设$\theta$是两个非零向量$\vec{a},\vec{b}$的夹角，已知对任意实数$t$，$|\vec{b}+t\vec{a}|$的最小值是$1$，【】

$A.若\theta确定，则|\vec{a}|唯一确定$

$B.若\theta确定，则|\vec{b}|唯一确定$

$C.若|\vec{a}|确定，则\theta唯一确定$

$D.若|\vec{b}|确定，则\theta唯一确定$

分析：利用$\Delta=0$，而不是$\Delta \leq 0$.
求解：
【法1】$|\vec{b}+t\vec{a}|≥1$，则有$\vec{b}^2+t^2\vec{a}^2+2\vec{a}\vec{b}t≥1$，即有$t^2a^2+2|\vec{a}||\vec{b}|\cos\theta\cdot t+b^2-1≥0$，

要保证对任意实数$t$，$|\vec{b}+t\vec{a}|$的最小值取到$1$，则必须$\Delta =0$，而不是$\Delta\leq 0$，

故解得$\Delta=4a^2b^2\cos^2\theta-4a^2(b^2 -1)=0$，则有$b^2-1=cos^2\theta$,故选B.

【法2】令$f(t)=|\vec{b}+t\vec{a}|^2=b^2+t^2a^2+2abt$，利用二次函数的最小值是1求解，倒是不容易出错。

感悟：同类题，已知开口向上的二次函数的值域是$[0,＋∞)$，则利用$\Delta=0$，而不是$\Delta \leq 0$.

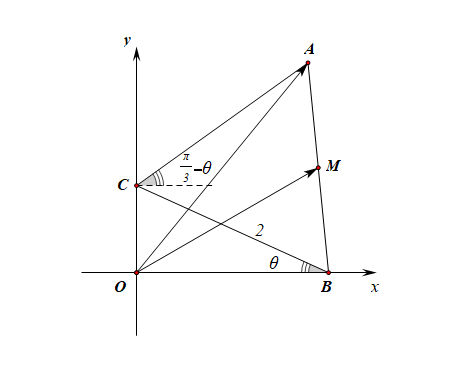
如图，等边$\triangle ABC$的边长为$2$，顶点$B$，$C$分别在$x$轴的非负半轴，$y$轴的非负半轴上滑动，$M$为$AB$中点，则$\overrightarrow{OA}\cdot \overrightarrow{OM}$的最大值为【】

$A.\sqrt{7}$ $B.\cfrac{5}{2}+\sqrt{7}$ $C.\cfrac{7}{2}$ $D.3+\cfrac{3\sqrt{3}}{2}$

法1：如图所示，设$\angle OBC=\theta$，则$\theta\in [0，\cfrac{\pi}{2}]$，则点$B(2cos\theta，0)$，$C(0，2sin\theta)$，

则点$A(2cos(\cfrac{\pi}{3}-\theta)，2sin(\cfrac{\pi}{3}-\theta)+2sin\theta)$，点$M(cos\theta+cos(\cfrac{\pi}{3}-\theta)，sin(\cfrac{\pi}{3}-\theta)+sin\theta)$

故$\overrightarrow{OA}\cdot \overrightarrow{OM}=(2cos(\cfrac{\pi}{3}-\theta)，2sin(\cfrac{\pi}{3}-\theta)+2sin\theta)\cdot (cos\theta+cos(\cfrac{\pi}{3}-\theta)，sin(\cfrac{\pi}{3}-\theta)+sin\theta)$

$=2cos(\cfrac{\pi}{3}-\theta)\cdot [cos\theta+cos(\cfrac{\pi}{3}-\theta)]+[2sin(\cfrac{\pi}{3}-\theta)+2sin\theta]\cdot [sin(\cfrac{\pi}{3}-\theta)+sin\theta]$

$=2cos(\cfrac{\pi}{3}-\theta)\cdot cos\theta+2cos^2(\cfrac{\pi}{3}-\theta)+2sin^2(\cfrac{\pi}{3}-\theta)+4sin(\cfrac{\pi}{3}-\theta)\cdot sin\theta+2sin^2\theta$

$=2(\cfrac{1}{2}cos\theta+\cfrac{\sqrt{3}}{2}sin\theta)cos\theta+2+4(\cfrac{\sqrt{3}}{2}cos\theta-\cfrac{1}{2}sin\theta)\cdot sin\theta+2sin^2\theta$

$=cos^2\theta+\sqrt{3}sin\theta cos\theta+2+2\sqrt{3}sin\theta cos\theta-2sin^2\theta+2sin^2\theta$

$=3\sqrt{3}sin\theta cos\theta+cos^2\theta+2$

$=\cfrac{3\sqrt{3}}{2}sin2\theta+\cfrac{1}{2}cos2\theta+\cfrac{5}{2}$

$=\sqrt{7}sin(2\theta+\phi)+\cfrac{5}{2}$

当$sin(2\theta+\phi)=1$时， $\overrightarrow{OA}\cdot \overrightarrow{OM}$最大值为$\cfrac{5}{2}+\sqrt{7}$，故选$B$.

法2：题源，另一种解法

【2019届高三理科数学三轮模拟试题】在$\triangle ABC$中，内角$A，B，C$所对的边分别为$a，b，c$，$AD$为$\angle BAC$的平分线，且满足$4\overrightarrow{AD}=\overrightarrow{AC}+3\overrightarrow{AB}$，$|\overrightarrow{AD}|=\sqrt{3}$，若$4c+a=8$，求$a$，$b$，$c$的值；

分析：由$4\overrightarrow{AD}=\overrightarrow{AC}+3\overrightarrow{AB}$，可得$3\overrightarrow{AD}-3\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{AD}$，

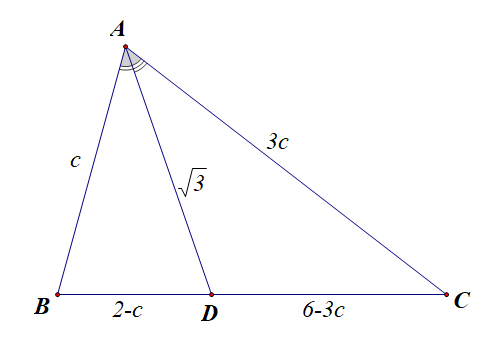
即$3\overrightarrow{BD}=\overrightarrow{DC}$，即$|CD|=3|BD|$，又$4c+a=8$，

则$a=8-4c=|BC|$，$|BD|=\cfrac{1}{4}|BC|=2-c$，$|CD|=6-2c$，

又由于$AD$为$\angle BAC$的平分线，由角平分线定理可知，

$\cfrac{BD}{CD}=\cfrac{AB}{AC}=\cfrac{1}{3}$，故$|AC|=3c$，

在$\triangle ABD$与$\triangle ACD$中，分别对$\angle BAD$和$\angle DAC$用余弦定理可得，

$\cfrac{3+c^2-(2-c)^2}{2\times \sqrt{3}c}=\cfrac{3+(3c)^2-(6-3c)^2}{2\times \sqrt{3}\times 3c}$

解得$c=\cfrac{5}{4}$，$b=\cfrac{15}{4}$，$a=3$。

解后反思：本题目需要特别注意向量系数的拆分技巧；

设点$A$，$B$，$C$不共线，则“$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角$\theta$为锐角”是“|$\overrightarrow{AB}$+$\overrightarrow{AC}$|>|$\overrightarrow{BC}$|”的【】条件

$A.充分不必要$ $B.必要不充分$ $C.充要$ $D.既不充分也不必要$

法1：从数的角度求解，由于点$A$，$B$，$C$不共线，则三点可以构成一个三角形$\triangle ABC$，

由向量加法可知，$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}$，则|$\overrightarrow{AB}$+$\overrightarrow{AC}$|>|$\overrightarrow{BC}$|

等价于|$\overrightarrow{AB}$+$\overrightarrow{AC}$|>|$\overrightarrow{AC}$-$\overrightarrow{AB}$|，两边平方，变形得到，

$4|\overrightarrow{AB}|\cdot |\overrightarrow{AC}|\cdot \cos\theta>0$，故$\cos\theta>0$，即$\theta$为锐角；

反之，当两个向量的夹角为锐角时，上述过程逆推成立，故选$C$;

法2：从形的角度求解；做一个向量三角形，让$\theta$变化，从动态图中就可以看出来；选$C$;

设$\vec{a}，\vec{b}$为单位向量，若向量$\vec{c}$满足$|\vec{c}-(\vec{a}+\vec{b})|=|\vec{a}-\vec{b}|$，则向量$|\vec{c}|$的最大值为多少？

法1：最容易想到两边平方，整理得到$\vec{c}^2-2(\vec{a}+\vec{b})\cdot \vec{c}+4\vec{a}\vec{b}=0$，

分解为$(\vec{c}-2\vec{a})(\vec{c}-2\vec{b})=0$，到此思路受阻。

法2：本题目用到绝对值不等式和均值不等式，

由题目得到$|\vec{c}-(\vec{a}+\vec{b})|=|\vec{a}-\vec{b}|\ge |\vec{c}|-|\vec{a}+\vec{b}|$，

即$|\vec{c}|\leq |\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|$，

接下来需要求$|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|$的最大值。

$|\vec{a}+\vec{b}|+|\vec{a}-\vec{b}|\leq \sqrt{2(|\vec{a}+\vec{b}|)^2+2(|\vec{a}-\vec{b}|)^2}$

$=\sqrt{2(2\vec{a}^2+2\vec{b}^2)}=2\sqrt{2}$，当且仅当$|\vec{a}+\vec{b}|=|\vec{a}-\vec{b}|$，

即$\vec{a}\perp\vec{b}$时取到等号，故$|\vec{c}|\leq 2\sqrt{2}$。

设$\vec{a}，\vec{b}$为单位向量，且$\vec{a}\perp \vec{b}$，若向量$\vec{c}$满足$|\vec{c}-(\vec{a}+\vec{b})|=|\vec{a}-\vec{b}|$，则向量$|\vec{c}|$的最大值为多少？

法1：采用上题的法2.

法2：由于$\vec{a}，\vec{b}$为单位向量，且$\vec{a}\perp \vec{b}$，

故设$\vec{a}=(1，0)，\vec{b}=(0，1)，\vec{c}=(x，y)$，

由$|\vec{c}-(\vec{a}+\vec{b})|=|\vec{a}-\vec{b}|$得到，

$|(x，y)-(1，1)|=|(1，-1)|$，即$\sqrt{(x-1)^2+(y-1)^2}=\sqrt{1+1}=\sqrt{2}$，

即$(x-1)^2+(y-1)^2=2$，

故$\vec{c}$的终点坐标对应的轨迹为圆心为$(1，1)$，半径为$\sqrt{2}$的圆，

又由于圆过圆心，则$|\vec{c}|$的最大值为圆的直径$2\sqrt{2}$。

已知$\vec{a}$，$\vec{b}$是单位向量，$\vec{a}\cdot \vec{b}=0$，若向量$\vec{c}$满足$|\vec{c}-\vec{a}-\vec{b}|=1$，则$|\vec{c}|$的最大值为()

A.$\sqrt{2}-1$ $\hspace{1cm}$ B.$\sqrt{2}$ $\hspace{1cm}$ C.$\sqrt{2}+1$ $\hspace{1cm}$ D.$\sqrt{2}+2$

法1：从形入手，条件$|\vec{c}-(\vec{a}+\vec{b})|=1$可以理解为如图的情况，

而$|\vec{a}+\vec{b}|=\sqrt{2}$，向量$\vec{c}$的终点在单位圆上，

故向量$|\vec{c}|$的最大值为$\sqrt{2}+1$，故选C。

法2：从数的角度，由题意得到$|\vec{a}|=|\vec{b}|=1，\vec{a}\cdot\vec{b}=0$，

所以$|\vec{a}+\vec{b}|=\sqrt{2}$，又因为$|\vec{c}-\vec{a}-\vec{b}|=1$，

所以$|\vec{c}-\vec{a}-\vec{b}|^2=\vec{c}^2-2\vec{c}\cdot(\vec{a}+\vec{b})+(\vec{a}+\vec{b})^2=1$，

设$\vec{c}$与$\vec{a}+\vec{b}$的夹角为$\theta$，

则$|\vec{c}|^2-2|\vec{c}|\times\sqrt{2}cos\theta+2=1$，

即$|\vec{c}|^2+1=2\sqrt{2}|\vec{c}|cos\theta\leq 2\sqrt{2}|\vec{c}|$，

即$|\vec{c}|^2-2\sqrt{2}|\vec{c}|+1\leq 0$，

解得$\sqrt{2}-1\leq |\vec{c}|\leq \sqrt{2}+1$。

法3：数形结合，由于$\vec{a}，\vec{b}$为单位向量，且$\vec{a}\perp \vec{b}$，

故设$\vec{a}=(1，0)，\vec{b}=(0，1)，\vec{c}=(x，y)$，

则$\vec{c}-\vec{a}-\vec{b}=(x-1，y-1)$，由$|\vec{c}-(\vec{a}+\vec{b})|=1$可得，

$\sqrt{(x-1)^2+(y-1)^2}=1$，即$(x-1)^2+(y-1)^2=1$，

即向量$\vec{c}$的终点坐标在圆心位于点$(1，1)$半径为$1$的圆上，

故$|\vec{c}|$的最大值是$\sqrt{2}+1$，

当然也可以知道$|\vec{c}|$的最小值是$\sqrt{2}-1$。

针对性训练

【2020人大附中高一试题向量部分第15题】已知向量$\vec{a}$，$\vec{b}$的夹角为$\cfrac{\pi}{4}$，$|\vec{b}|=\cfrac{\sqrt{2}}{2}$，且对于任意的$x\in R$，都有$|\vec{b}+x\vec{a}|\geqslant |\vec{b}-\vec{a}|$，则$|\vec{a}|$=_____________。

分析：由于对于任意的$x\in R$，都有$|\vec{b}+x\vec{a}|\geqslant |\vec{b}-\vec{a}|$，

则$|\vec{b}+x\vec{a}|^2\geqslant |\vec{b}-\vec{a}|^2$对于任意的$x\in R$都成立，

即$(\vec{b}+x\vec{a})^2\geqslant (\vec{b}-\vec{a})^2$对于任意的$x\in R$都成立，

即$\vec{b}^2+2x\vec{a}\cdot\vec{b}+x^2\cdot \vec{a}^2\geqslant \vec{b}^2+\vec{a}^2-2\vec{a}\cdot\vec{b}$，

即$\vec{a}^2\cdot x^2+2\cdot |\vec{a}|\cdot \cfrac{\sqrt{2}}{2}\cdot \cfrac{\sqrt{2}}{2}x+2\cdot |\vec{a}|\cdot \cfrac{\sqrt{2}}{2}\cdot \cfrac{\sqrt{2}}{2}-\vec{a}^2\geqslant0$，

由于$\vec{a}\neq \vec{0}$，故上式是关于$x$的二次不等式，注意：$\vec{a}^2=|\vec{a}|^2$，

即$|\vec{a}|^2\cdot x^2+|\vec{a}|\cdot x+|\vec{a}|-|\vec{a}|^2\geqslant 0$对于任意的$x\in R$都成立，

故$\Delta \leqslant 0$恒成立，即$\Delta=|\vec{a}|^2-4|\vec{a}|^2(|\vec{a}|-|\vec{a}|^2)\leqslant 0$，

即$1-4(|\vec{a}|-|\vec{a}|^2)\leqslant 0$，即$(2|\vec{a}|-1)^2\leqslant 0$，

又由于$(2|\vec{a}|-1)^2\geqslant 0$，故只能$(2|\vec{a}|-1)^2=0$，

即$|\vec{a}|=\cfrac{1}{2}$。

posted @ 2019-02-10 13:45 静雅斋数学阅读(1903) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

平面向量习题|高阶

前言

相关定理

典例剖析

针对性训练

公告